'머신러닝을 위한 수학: 선형대수' 시리즈는 Mathematics for Machine Learning과 Gilbert Strang 교수님의 Linear algebra를 참고했습니다.
Vector spaces
벡터 공간은 벡터로 이뤄진 공간으로, 선형대수를 공부할 때 주로 다루게 될 기본 공간입니다. 벡터 공간에서는 두 가지 연산자(덧셈, 곱셈)가 정의됩니다. 이를 통해 벡터들은 서로 더해지거나, 스칼라 값이 곱해질 수 있는데요. 벡터 공간은 다음과 같은 특징이 있습니다.
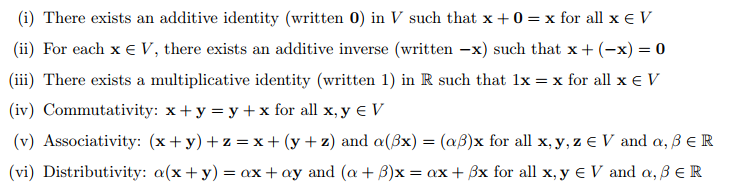
머신러닝에서 주로 다루게 될 공간은 Euclidean space로, 실수(Real numbers)로 이뤄진 벡터가 구성하는 공간입니다. $R^n$이라고 주로 부르며, 크기가 $n * 1$인 행렬로 생각해도 무방합니다. 벡터 공간이기 때문에 위에서 정의한 성질들을 모두 만족합니다.
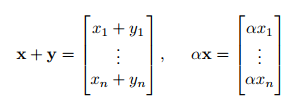
Subspaces
벡터 공간은 다른 벡터 공간을 담을 수 있는데, 이 때 담겨진 공간을 V의 subspace라고 부릅니다. Subspace는 아래와 같은 특징을 가지고 있습니다(덧셈과 곱셈에 대해 닫힌 공간). 모든 벡터 공간은 subspace를 가지며, 공통적으로 {0}을 subspace로 가집니다.

그렇다면, 벡터 공간 V의 subspace인 U, W를 서로 더한다면 어떻게 될까요??
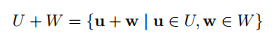
U, W가 V의 subspace였으므로, 자연스럽게 U+W도 V의 subspace가 됩니다. 위의 예시를 통해 direct sum(⊕)이라는 연산자를 살펴봅시다. U와 W의 교집합에 속하는 벡터가 없을 때 두 subspace를 더하는 것을 direct sum(⊕)이라고 부릅니다. 일반적인 두 개의 subspace의 합은 아래와 같이 표현하는데요.
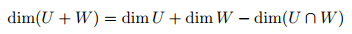
두 개의 subspace의 교집합이 없으면 아래와 같이 표현가능하고, 이를 direct sum이라고 부르는 것이죠.
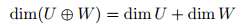
'머신러닝 수학 > 선형대수' 카테고리의 다른 글
| Mathematics for Machine Learning: Metric & Normed spaces (0) | 2023.03.07 |
|---|---|
| Mathematics for Machine Learning: Linearity & Linear maps (0) | 2023.03.06 |
